SolutionShow Solution `1/ √3 √2 1` = `1/ (√3 √2) 1 xx (√3 √2) 1/ (√3 √2) 1` = ` (√3 √2 1)/ (√3 √2)^2 (1)^2` = ` (√3 √2 1)/ (√3)^2 2√6 (√2)^2 1 ` = ` (√3 √2 1)/ (3 2√6 2 1)` = ` (√3 √2 1)/ ( 4 2√6 )` = ` (√3 √2) 1/ 2 ( 2 √6 )`Is done on EduRev Study Group by Class 9 Students The Questions and Answers of Rationalize the denominator of 30/ 5√3−3√5?EduRev Class 9 Question is disucussed on EduRev Study Group by 147 Class 9 Students

Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation
Rationalise the denominator of ((5 sqrt(3)-4sqrt(2))/(4sqrt(3)+3sqrt(2)))
Rationalise the denominator of ((5 sqrt(3)-4sqrt(2))/(4sqrt(3)+3sqrt(2)))-Share It On Facebook Twitter Email 1 Answer 1 vote answered by Tahseen Ahmad (300k points) selected by ShasiRaj Best answer 3/2 √5 Multiply by √5 both numerator and denominator ← PrevRationalise the denominator and simplify 7 √3/√10√3 2√5/√6√5 3√2/√153√2 Share with your friends Share 1 Dear Student, Please find below the solution to the asked query Rationalise the denominator 7 3 10 3 2 5 6 5



Www Jstor Org Stable 10 4169 Math Mag 2 121
A easy way to understand the method to rationalize the denominator Rationalize the denominator (√2√3)/(√2√3) and ((53√14))/((72√14))Find right answers right now!Radicals that have Fractions – Simplification Techniques A radical can be defined as a symbol that indicates the root of a number Square root, cube root, fourth root are all radicals This article introduces by defining common terms in fractional radicals If n is a positive integer greater than 1 and a is a real
When we rationalize the denominator in a fraction, then we are eliminating any radical expressions such as square roots and cube roots from the denominator In this article, let's learn about rationalizing the denominator, its meaning, and methods with solved examplesWhat you have written is actually 1 2 3 5 Why?Jul 24,21 √2/2√3 rationalize the denominator?
Rationalise the denominator and simplify 10/3√5 (2 marks) First of all, you need to read the question really carefully and look at how many marks it is worth The question is worth two marks and it is asking you to do two things firstly, you need to 'rationalise the denominator', and then you need to 'simplify' your answer(2√3√5)/(2√23√3) Rationalise the DenominatorRationalise the denominator 3 − 2 3 2 Hard




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation
Question Rationalize the denominator 3 2 V17 3 2 √17 (Simplify your answer Type an exact This question hasn't been solved yet Ask an expert Ask an expert Ask an expert done loading Show transcribed image text Expert Answer Who are the experts?Rationalise the denominator 3/(2 √5) rationalisation; Rationalize the denominator for each of the following expressions a 1/(2 √3)




Rationalize The Denominator Of 3 Minus Root 2 By 3 Root 2 Brainly In




Simplify By Rationalising The Denominator 2 6 5 3 5 2 6
Isai Crosby 10 September, 0048 0 (√2 3) / 7 Stepbystep explanation To rationalize the denominator, we need to multiply by the conjugate 1 / (3 √2) * (3 √2) / (3 √2) (3 √2) / (9 √4) (3 √2) / (9 2) (√2 3) / 7Multiplying both numerator and denominator with 2 − 3 = 2 3 ( 2 − 3 ) ( 6 ) ( 2 − 3 ) = 2 2 − 3 3 6 2 − 6 3 Rationalise the denominator of 1/√3√2 and hence evaluate by taking √2 = 1414 and √3 = 1732,up to three places of decimal



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community
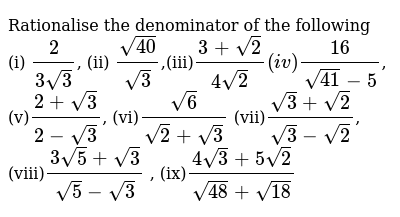



Rationalise The Denominator Of The Following I 2 3sqrt3
This discussion on Rationalize the denominator of 30/ 5√3−3√5?The bottom of a fraction is called the denominator Numbers like 2 and 3 are rational 🔴 Answer 2 🔴 on a question Rationalize the denominator of 73√2 the answers to answerhelpercom




Rationalize The Denominator 2 3 2 3




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download
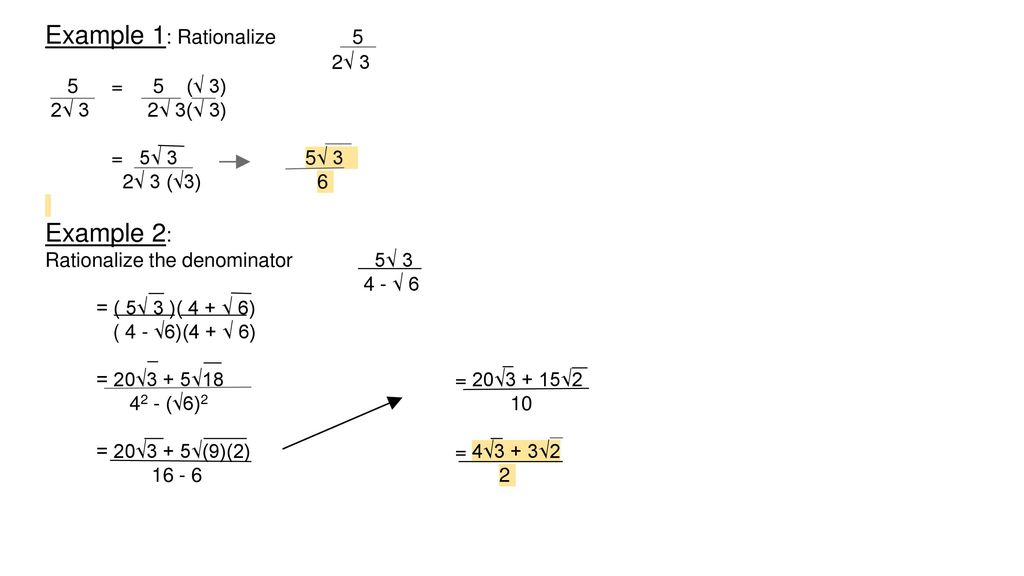
A81 Rationalise a surd in the denominator Rationalise a denominator means getting rid of surds from the bottom of a denominator To rationalise surds in the denominator 1 Multiply both numerator and denominator by the surd (in the denominator) 2 Simplify the expression Example A81a Rationalise the denominator of 1 √8 √8 √=22 1 √8Convention re the order of operations;Rationalize and simplify the expression12√3 √2√3√5 2−√3 1√5 1√3 12√3=12√3×2−√32−√3Now a−b×ab=a2−b2=2−√34−3=2−√31=2−√3



Rationalize Denominator 7 3 2 7 3 2 Brainly In




Ua1q0rjacmga5m
More questions about Science & Mathematics Rationalise the denominator of 1/((8 5√2)) You are here Simplify (7√3)/(√10 √3)−(2√5)/(√6 √5)−(3√2)/(√15 3√2) Multiple Choice Questions Chapter 1 Class 9 Maths Example 17 If a and b are rational numbers and (√11 −Free rationalize denominator calculator rationalize denominator of radical and complex fractions stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy




After Rationalizing The Denominator Of Dfrac 4sqrt 3 5sqrt 2 Sqrt 48 Sqrt 18 And Simplifying We Get Dfrac A Bsqrt 6 15 Then The Value Of Atimes B Is




Rationalise The Denominator Of 2 Sqrt 3 Sqrt 5 Youtube
Multiply both numerator and denominator with √3 it will be rationalize (√5×√3)/(2×√3×√3)= √15/6A Rationalise a surd expression • To rationalise expression of the form (a √b ) in the denominator, multiply both numerator and denominator by (a √b )How do I rationalise the denominator, 1/√2√3√5?




Rationalize The Denominator Expii




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66
Example Rationalise the denominator for 2/ (√35) In the given example, the denominator has one radical and a whole number added to it Thus, the conjugate of √3 5 is √3 – 5 Multiplying numerator and denominator by the conjugate of √3 5 ⇒ By the formula (ab) (ab) = a 2 – b 2 , we can write;Rationalise the denominator 52√3/74√3 Ask questions, doubts, problems and we will help youJust like 12/213 = 613=10 The only denominator in this expression is the surd √2 To remove this surd, we just need to multiply the numerator and denominator by √2, thus we have 1 2 × 2 2



Chapter 5 Radical Expressions And Equations Ppt Download
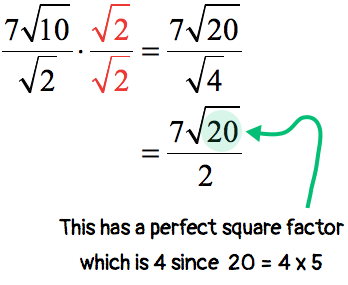



Rationalizing The Denominator Chilimath
Rationalising the denominator Rationalise the denominator, 1) 5 √3 2) 5 √6 3) 2 √3 4) 5 √7 5) 4 √3 6) 4 √6 7) 3 √2 8) 3 √3 9) 4 √2 10) 4 √2 11) 4 Rationalise the denominator of the following √32/√32 Solution To Rationalise Denominator of √32/√32Method ⇒ ⇒ ⇒ ⇒ ⇒ Hence, The rationalized form is (74√3) Both your results are correct and identical in meaning There are many ways to show the answer For example, − √2 √5 2 ∗ √3 √7 2 − 2 5 2 ∗ 3 7 2 So you are really asking a question about what is conventional in presentation The seemingly childish answer to that question is that you should do whatever your teacher
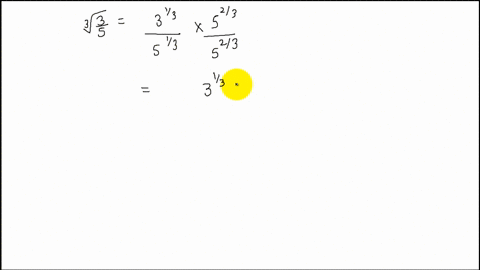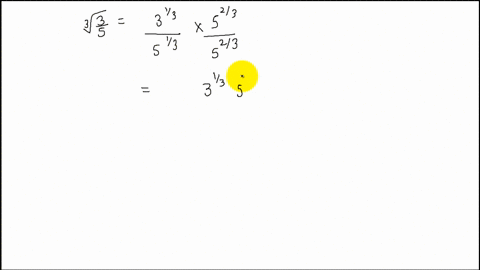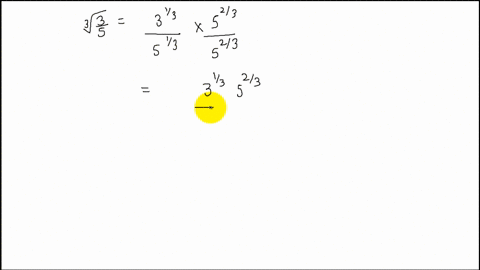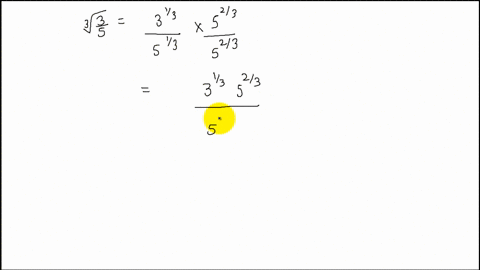



Solved Rationalize The Denominator Frac 3 2 S
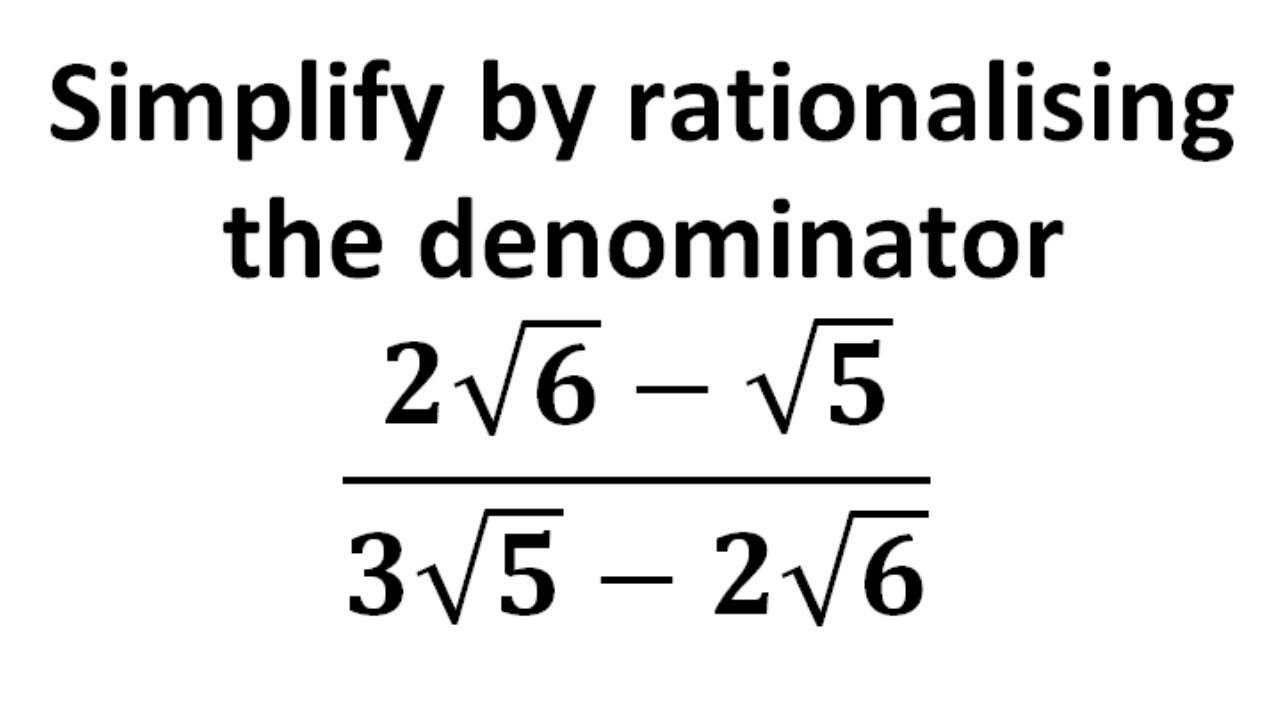



Simplify By Rationalising The Denominator 2 Root 6 5 3 Root 5 2 Root 6 Youtube
Solution Step 1 We have to rationalize the denominator Here we have √6 (in the form of √a) Then we have to multiply the numerator and denominator by √6 Step 2 By multiplying the numerators and denominators of first and second fraction , we get Step 3Rationalize the Denominator "Rationalizing the denominator" is when we move a root (like a square root or cube root) from the bottom of a fraction to the top Oh No! Rationalise the denominator of 2/√3 √5 Share with your friends Share 0 2 3 5 =2 5




How To Rationalize The Denominator 14 Steps With Pictures




Rationalize The Denominator 6 3 2 2 3 Brainly In
Experts are tested by Chegg as specialists in their subject areaSolutionShow Solution ` 2 √3 / 2 √3 xx 2 √3 / 2 √3 ` = ` ( 2 √3 )^2/ (2)^2 (√3)^2 = 4 3 4√3/ 4 3 ` = ` 7 4√3 /1` = 7 4√3 Concept Simplifying an expression by rationalization of the DenominatorRationalize the denominator of \frac{1}{2\sqrt{3}} by multiplying numerator and denominator by 2\sqrt{3} Rationalize the denominator of 2 − 3 1 by multiplying numerator and denominator by 2



1




Rationales The Denominator And Simplify Sqrt 3 Sqrt 2 Sqrt 3 Sqrt 2 Ii 5 2sqrt 3 7 4sqrt 3 Iii 1 Sqrt 2 3 2sqrt 2 2sqrt 6 Sqrt 5 3sqrt 5 2sqrt 6 V 4sqrt 3 5sqrt 2 Sqrt 48 Sqrt 18 Vi 2sqrt 3 Sqrt 5 2sqrt
👍 Correct answer to the question Rationalise the denominator 2−√3 2√3 eanswersin Rationalise the denominator of each of the following (i) 3√5 (ii) 3/2√5 (iii) 1/√12 (iv) √2/√5 asked Apr 15 in Number System by Madhuwant ( 381k points) rationalisation Answers 1 continue Mathematics, 30, shonesam98 Apinhole camera is made out of a lighttight box with a piece of film attached to one side and pinhole on the opposite side the optimum diameter d (in millimeters) of the pinhole can be modeled by d=19 (55 x 10^4) l) ^1/2, where l is the length of the camera box (in




Multiplying And Dividing Radical Expressions




Rationalize The Denominator Meaning Methods Examples
Rationalize the denominator 2√3/ 2√3?Rationalize the denominator of \frac{3}{2\sqrt{3}} by multiplying numerator and denominator by 2\sqrt{3} Rationalize the denominator of 2 3 3 by multiplying numerator and denominator by 2 Example Rationalise the denominator of 17 3 2 17 3 2 = 17 3 2 × 7 − 3 27 − 3 2 = 7 − 3 2 7 3 2




Rationalise The Denominator 2 3 2 3




Rationalize The Denominator Squareroot 1 2 Chegg Com
Rationalise the denominator 3√2/3√2 Ask questions, doubts, problems and we will help youAre solved by group of students and teacher of Class 9, which is also the largest student community of Class 9Rationalise the denominator of 2√3/2√3 Home Class 9th Maths 9th Rationalise the denominator of 2√3/2√3 by John_ka_Sena Unbeaten Ingenious




Rationalise The Denominator Of The Following I 2 3sqrt3 Ii Sqrt40 Sqrt3 Iii 3 Sqrt2 4sqrt2 Iv 16 Sqrt41 5 V 2 Sqrt3 2 Sqrt3 Vi Sqrt6 Sqrt2 Sqrt3 Vii Sqrt3 Sqrt2 Sqrt3 Sqrt2 Viii 3sqrt5 Sqrt3 Sqrt5 Sqrt3 Ix 4sqrt3




Rationalize The Denominator Meaning Methods Examples
To rationalise the denominator without chainging the value of the equation, multiply both the numerator and denominator by the value of the denominator( (5√2)/( This is the key to eliminating square roots from the denominator Note that (1 − √2 √3) is only a partial conjugate for (1 √2 √3) Multiplying these two expressions will eliminate terms in √2 but leave terms in √3 If we want to rationalise the denominator, we will also need to multiply by some expression of the form a b√3Here we have 2√3 in the denominator, to rationalize the denominator we have multiply the entire fraction by its conjugate Conjugate of 2√3 is 2√3 Step 2 (i) In the numerator we have (1 2√3) (2 √3) By multiplying these terms we get, 2 6 5 √3




Example 18 Rationalize The Denominator Of 1 2 Root 3



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community



Rationalize The Denominator I 1 5 Ii 2 3 7 Iii 1 3 2 Iv 1 3 5 2 2 V 12 4 3 2 Sarthaks Econnect Largest Online Education Community




Intro To Rationalizing The Denominator Algebra Video Khan Academy




After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is
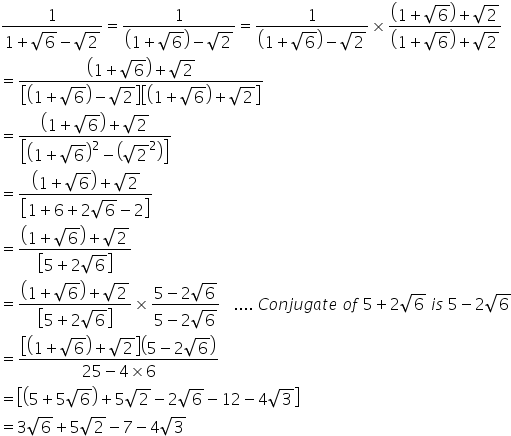



Rationalise The Denominator Of The Expression Mathematics Topperlearning Com Hvx3khh




Example Rationalise The Denominator Of 1 7 3 Root 2



Simplifying By Rationalising The Denominator 4 2 3 7 Studyrankersonline



How To Rationalize The Denominator Of 1 2 1 3 2 1 3 Quora



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Rationalize 2 3 5 2 2 3 3 Brainly In
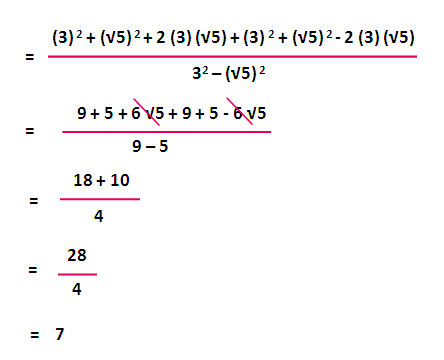



Rationalizing The Denominator With Variables




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation




Example 2 Rationalize Denominators Of Fractions Simplify Ppt Download




Rationalize The Denominator 3 77 V10 A 10 V Chegg Com



1
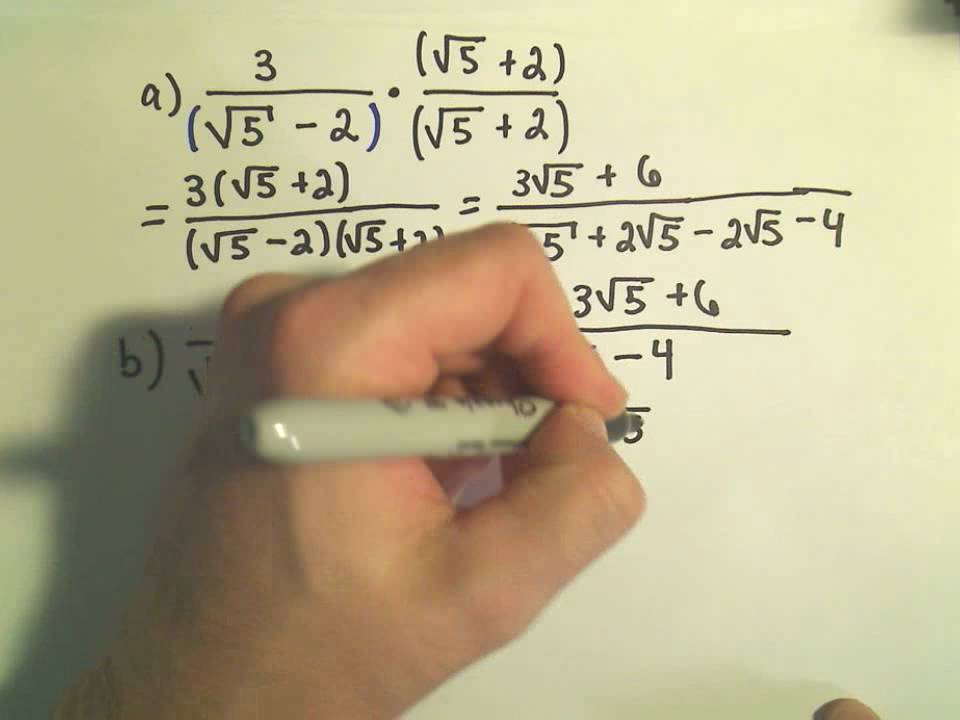



Rationalizing The Denominator Example 1 Youtube



Simplifying By Rationalising The Denominator 1 3 2 5 Studyrankersonline




Rationalize 1 7 3 2 Maths Questions




Rationalise The Denominator Of 1 Root3 Root2 Brainly In




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation



Www Jstor Org Stable 10 4169 Math Mag 2 121



Simplifying By Rationalising The Denominator 3 5 3 2 5 3 Studyrankersonline




Rationalizing Denominator Google Worksheets Teaching Resources Tpt



1




After Rationalizing The Denominator Of 3 12 2 3 And Simplifying We Get 2 6 3 2 M 3 5 Then The Value Of M Is




How To Rationalize The Denominator 14 Steps With Pictures



Rationalise The Denominator In Each Of The Following And Hence Evaluate By Taking 2 1 414 3 1 732 And 5 2 236 Up To Three Places Of Decimal Studyrankersonline
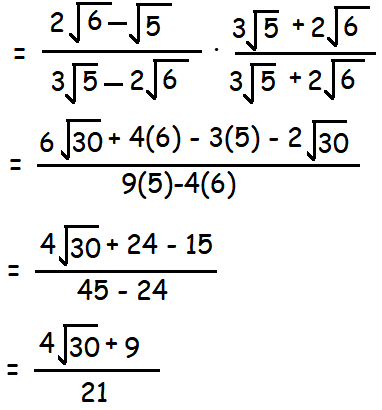



Practice Problems On Rationalizing Denominator
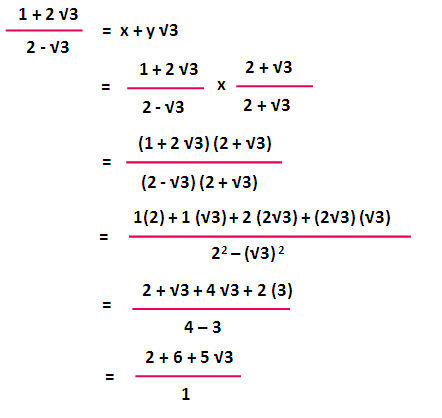



Rationalizing The Denominator With Variables




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium




How To Solve Surds 2 Four Essential Surd Techniques Suresolv
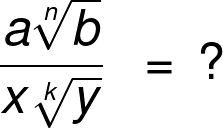



Rationalize Denominator Calculator




Rationalise The Denominator 1 1 2 3 Maths Number Systems Meritnation Com




Rationalise The Denominator Of 1 8 5 2 Rationalise The Denominat
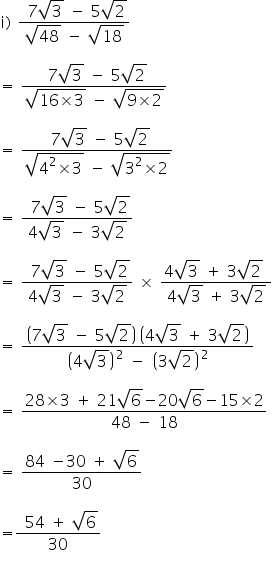



Sir Pls Solve The Following Problem Rationalize The Denominator 7 3 5 2 2 6 5 48 18 3 5 2 6 1 2 3 1 3 2 2 3 1 Mathematics Topperlearning Com Lh6vmmyy




How To Rationalize The Denominator 14 Steps With Pictures




How Do You Simplify Sqrt 15xy 3sqrt 10xy 3 Socratic



How To Rationalize Math Frac 1 Sqrt 7 Sqrt 3 Sqrt 2 Math Quora




Ex 1 5 5 Rationalize Denominators Of I 1 Root 7 Ii 1 Root6
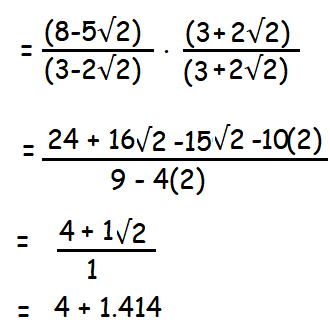



Practice Problems On Rationalizing Denominator




7 5 Root 3 5 Root 2 Rationalise The Denominator Youtube




4 Rationalize The Denominator And Simplify 2 5 A Chegg Com




Rationalise The Denominators 1 3 Root 2 2 1 Root 6 Root 5 3 16 Root 41 5 Youtube




Rationalize Denominator Calculator



Q Tbn And9gcsb2rnpibjsemfefshm1leviszzhattq67fri0obpzhq J Lxfh Usqp Cau




Rationalize The Denominator Expii



1 Multiply 1 7 3 2 Rationalize The Denominator Ii 5 7 2solve Ii 3 2 1 3x 511 Snapsolve




R D Sharma Solutions Class 9th Ch 3 Rationalisation Exercise 3 2




Rationalize The Denominator 12 5 3 And Hence Find The Value Of A B In 12 5 3 A 5 B 3




Rationalise The Denominator 2 Root 5 Root 3 Root 2plz Give Complete Solution Plz Don T Spam




3 2 1 2 5 3 Rationalise This Term In Briefly Brainly In




Rationales The Denominator And Simplify Sqrt 3 Sqrt 2 Sq




Multiplying And Dividing Radical Expressions




Rd Sharma Solutions For Class 7 Maths Chapter 4 Rational Numbers Exercise 4 2 Access Free Pdf




How To Rationalize Math Frac 1 Sqrt 2 Sqrt 3 Sqrt 5 Math Quora
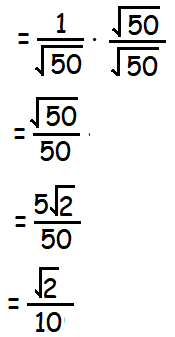



Practice Problems On Rationalizing Denominator




After Rationalizing The Denominator Of 2 6 5 3 5 2 6 And Simplifying We Get 9 4 A B Then The Value Of A B Is




Solved Rationalize The Denominator And Simplify The Follo Chegg Com
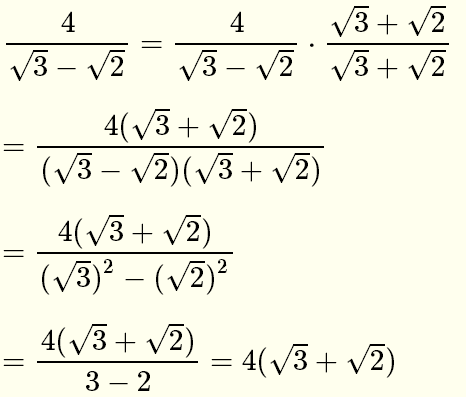



Mwydy6n8tskywm
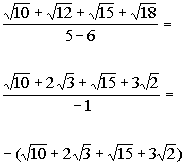



Rationalizing Denominators And Numerators Of Radical Expressions



Surds Mathematics Gcse Revision




Rationalize The Denominator 2 3 1




Example 19 Rationalize The Denominator Of 5 3 5 Examples




Cuoafsyhuwt38m




Rationalise The Denominator 2 3 2 Brainly In




Chapter 3 Rationalisation Fraction Mathematics Rational Number



Rationalise The Denominator Of 1 3 2 And Hence Evaluate By Taking 2 1 414 And 3 1 732 Up To Three Places Of Decimal Studyrankersonline




Rationalise The Denominator Of The Following A 2 3sqrt 3 B Sqrt 40 Youtube




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium



How To Rationalise The Denominator 1 2 3 5 Quora
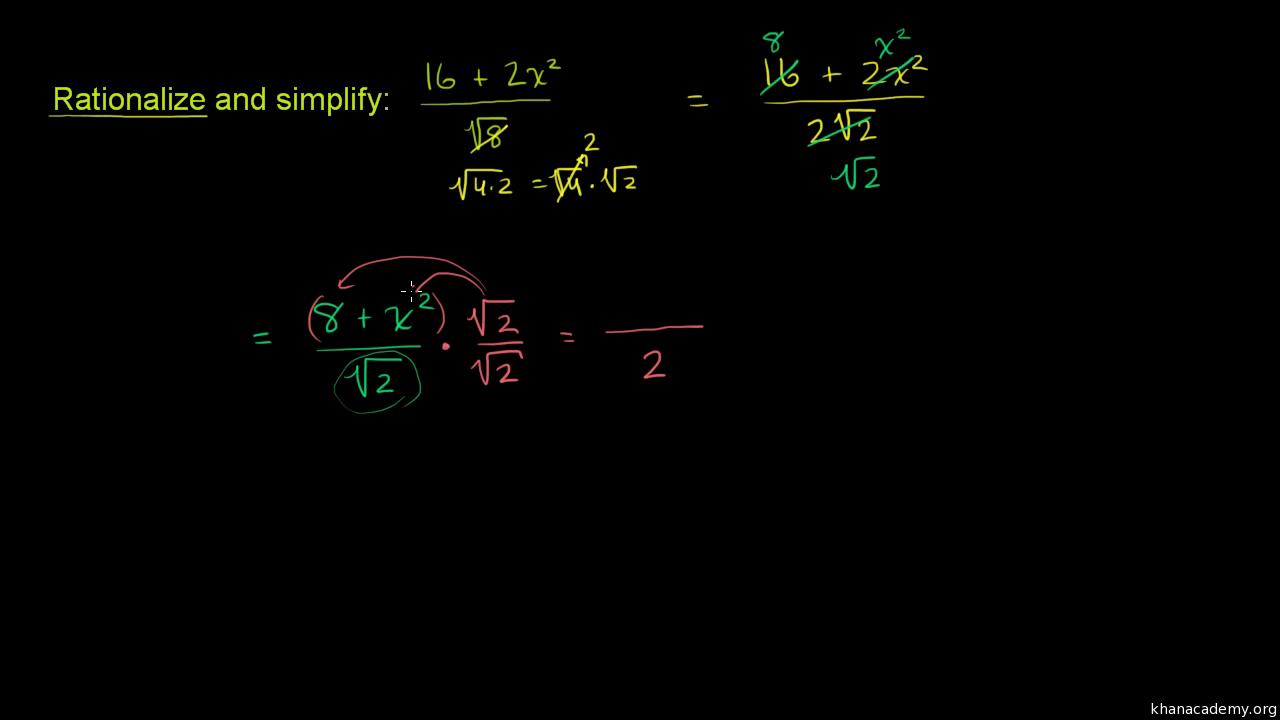



Worked Example Rationalizing The Denominator Algebra Video Khan Academy




2 Is Divided By 3 Root 3 By Rationalizing The Denominator Brainly In




How To Rationalize Math Frac 1 Sqrt 7 Sqrt 3 Sqrt 2 Math Quora
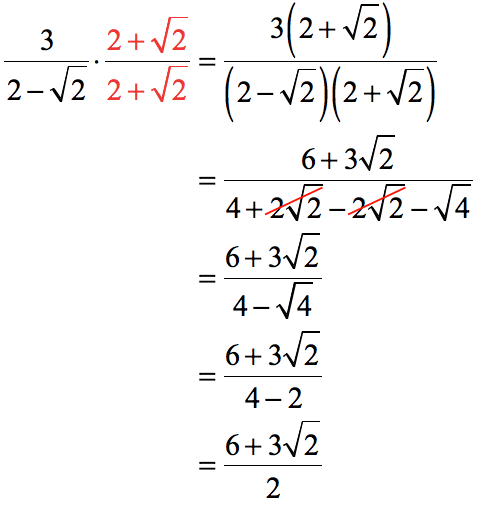



Rationalizing The Denominator Chilimath



0 件のコメント:
コメントを投稿