Simplify √(i) ( 3 √3 √) (2 2 √) (ii) ( 11 √7 ) ( √11 7 ) (iii) ( 5 2 )2 √(iv) ( 2 √2 √ 33 11 √) ( 5 √3 22 6 √11 ) (v) 16 √15 √÷ 4 3 (vi) 2 5 X 6 √5 16 Rationalise the denominator (i) 5 √3 − √5 1 (ii) 7−3√2 73√2 (iii) 5 √2 3√2 (iv) 2 − √3Express in the form ab√3, (1√3)(2√3) 109√3 Express in the form ab√3, (4√3)(12√3) 4324√3 Rationalise the denominator 3/2√54 4√10/9 Rationalise the denominator 4√/3√18 5√21/6 Rationalise the denominator 3√175/2√27 √5/5Click here👆to get an answer to your question ️ If x and y are rational numbers such that 2 √(3)2 √(3) = x y√(3) , find the value of x and y

Rationalize The Denominator Expii
Rationalise the denominator of (3-sqrt(2))/(3sqrt(2))
Rationalise the denominator of (3-sqrt(2))/(3sqrt(2))-The rationalizing factor of 2√3 is √3 2√3 × √3 = 2 × 3 = 6 Rationalize the Denominator Meaning Rationalizing the denominator means the process of moving a root, for instance, a cube root or a square root from the bottom of a fraction to the top of the fraction1/x cannot be 2 root 3, you have to rationalise the Denominator So your answer which is I guess 24/3 is wrong Nikhil Chouti 27 Points 2 years ago x=2√3 1/x=1/2√3 which upon rationalising we get 2√3 x^31/x^3=2√3 2√3 =4 Therefore 4 is the answer




The Simplest Rationalisation Factor Of 2sqrt 2 Sqrt 3 Youtube
Rationalise4÷2√3√7 Sol4 2 √3 √7= 42 √3 √7Rationalising factor of the denominator is 2 √3 √7= 12 √3 √7 x 2 √3 √7 2 √3 √7 Rationalise 4÷2√3√7 Please scroll down to see the correct answer and solution guide Right Answer is SOLUTION Sol 4 / (2 √3 √7) = 4/(2 √ Simplify expressions involving algebraic fractions and square roots To simplify an algebraic expression you have to gather all like terms together eg simplify 2 x − 1 − 1 x 1 step 1) 2 ( x 1 ) x − 1 − 1 ( x − 1 ) x 1 step 2) 2 x 2 x − 1 − x − 1 x 1 step 3) 2 x 2 x 1 (x − 1)(x1) = x 3 x 2 − 1 To rationalise a denominator you need to times it by itselfRationalise the denominator √ A (2√3 2√3) B √ C − √ − √ D 𝟗√ 9) The point A(– 5 , – 8) is found in A Quadrant I B Quadrant II C Quadrant III D Quadrant IV 10) A set of points are collinear if they A form lines that intersect B form a rightangled triangle
Study the following Mathematics past questions and answers for JAMB, WAEC, NECO and Post UTME Prepare yourself with official past questions and answers for your upcoming examinationsRationalize the denominator (2 √3)/(2 √3) = x y√3 and find the value of x and y Solution Now we have to compare the final answer with RHS The values of x and y are 7 and 4 respectively Apart from the stuff given above, if you need any other stuff in math, please use our google custom search hereClick here👆to get an answer to your question ️ The value of 4√(3)4/√(3)1 2 √(3)/2 √(3) is Join / Login > 9th > Maths > Number Systems > Rationalisation Rationalise the denominator and simplify 2
TOP 10 SURDS SKILLS 1 Simplify √60 2 Simplify 3√5−√5 3 Simplify √30×√6 4 Simplify 2√18×3√2 5 Expand and simplify √3(2 √3) 6 Expand and simplifyI am going to use sqrt to represent square root The expression is (2 x 3 ) / sqrt (3) Lets rewrite this as 2 x (3/sqrt(3)) Since sqrt(3) x sqrt(3) = 3, We can deduce sqrt (3) = 3 / sqrt(3) Lets substitute this in the expression above We get 2 x Please try and explain this to me, Im stuckQuestion 1) Expand the brackets using the distributive property √18 2(3) = √18 6 To simplify √18, think of two numbers that when multiplied togethe



How To Rationalise The Denominator 1 2 3 5 Quora




Surds A Plus Topper
√ 3 = 2 √ 3 5 √ 3 = 2 5 Note that the 2 2 The way to rationalise a surd on the denominator is to multiply both the numerator and denominator by the surd Examples 1 Problem RationaliseExercise 32 Question 1 Rationalise the denominator of each of the following (ivii) (i) (ii) (iii) (iv) (v) (vi) (vii) Answer (i) As there is √5 in the denominator and we know that √5 x √5 = 5 So, multiply numerator and denominator by √5, Rationalise the denominator of 2√3 / 2√3 2 See answers khanujarashmit khanujarashmit Solution is attached below But we should multiply both numerator & denominator with 2√3 (rationalising factor) So I got the answer as 7 tapdiyaunnati tapdiyaunnati




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation




Example 19 Rationalize The Denominator Of 5 3 5 Examples
Rationalise 2/2√3 √3/3 5√5/√ 5/2 √3 x √5 √15 5√25 25 3√45√4 16 6√32√3 4√3 √12√27 5√3 THIS SET IS OFTEN IN FOLDERS WITH Algebra 7 terms 6√32√3 4√3 √12√27 5√3 THIS SET IS OFTEN IN FOLDERS WITH Algebra 7 terms IlluminatiAxar Trigonometry and pythagoras 7 termsA Rationalise a surd expression • To rationalise expression of the form (a √b ) in the denominator, multiply both numerator and denominator by (a √b ) • To rationalise expression of the form (a √b ) in the denominator, multiply both numerator and denominator by (a √b ) • Use (a √b ) (a √b ) = a 2 bTO PROVE 1/(2√3) is irrational We can rationalize the denominator of the above expression, & then we can proceed with our proof After rationalization 1 / (2√3) * (2√3) / (2√3) = (2




Rationalize 1 7 3 2 Maths Questions




Rationalise The Denominator 2 3 2 Brainly In
E x e r c i s e 3 2 1 Question Rationalise the denominator of each of the following (ivii) (i) (ii) (iii) (iv) (v) (vi) (vii) Answer (i) As there is √5 in the denominator and we know that √5 x √5 = 5 (2 ) (2 ) Answer (2√3) (2√3) = (2)2 (√3)2 (ab) (ab) = a2 –b2 = 4 – 3 = 1 2SCHOLAR Study Guide National 5 Mathematics Assessment Practice Topic 8 Surds and indices Authored by Margaret Ferguson HeriotWatt University Edinburgh EH14 4AS, United KingdomCommon factor of 2, √14 and 6 do not Write the numerator and denominator as two separate square roots using the Quotient Rule for Radicals To rationalize the denominator of a fraction containing a square root, simply multiply both the √3 2 ∙√3 2 √3



How To Rationalize The Denominator Of 1 2 1 3 2 1 3 Quora




Rationalise The Denominator 1 1 2 3 Maths Number Systems Meritnation Com
Answer Let √5 – 2 be a rational number Here, x is a rational number ⇒ 9 – x 2 is an irrational number ⇒ x 2 is an irrational number ⇒ x is an irrational number But we have assume that x is a rational number ∴ we arrive at a contradiction So, our assumption that √5 – 2 is a rational number is wrongAnswer choices rational irrational s Question 22 SURVEY 30 seconds Q Is √64 rational or irrational?Rationalise the denominator answer choices √12 (4√3)/3 √3 (2√3)/3 s Question 13 SURVEY 60 seconds Q Rationalise the denominator answer choices Is √2 rational or irrational?




How To Rationalize The Denominator 14 Steps With Pictures




Rationalise The Denominator 2 Root 5 Root 3 Root 2plz Give Complete Solution Plz Don T Spam
Rationalise the denominator of 1/√3√2 and hence evaluate by taking √2 = 1414 and √3 = 1732,up to three places of decimal asked in Class IX Maths by muskan15 (Pupils should be taught to calculate exactly with fractions, {surds} and multiples of π ;• An expression that involves irrational roots is in SURD FORM eg 2√3 • √3 2 and 3 √2 are CONJUGATE/COMPLEMENTARY surds – needed to rationalise the denominator SIMPLIFYING √ = ×√ √ = √ √ RATIONALISING THE DENOMINATOR (removing the surd in the denominator)



After Rationalising The Denominator Of 7 3 3 2 2 We Get The Denominator As A 13 B 19 C 5 D 35 Sarthaks Econnect Largest Online Education Community




Example Rationalise The Denominator Of 1 7 3 Root 2
Transcript If x = 1/(2 − √3), find the value of x3 − 2x2 − 7x 5 Let us first rationalise x x = 1/(2 − √3) = 1/(2 − √3) × (2 √3)/(2 √3• simplify surd expressions involving squares (eg 12 = √(4 × 3) = √4 × √3 = 2√3) and rationalise single term denominators (NCA) • apply systematic listing strategies including use of the product rule for counting (NCA) Return to overview SKILLS Suggested resourcesRationalise x, x=(2√3)/(2√3)(2 4 2√3 5 = 2(2 √3)(2 √3) 5 = 2(1) 5 = 3 So the required answer is 3 Related Questions Find the irrational numbers between root 2 and root 3;




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising




7 5 Root 3 5 Root 2 Rationalise The Denominator Youtube
9 Write a pair of irrational numbers whose difference is irrational Answer √3 2 and √2 – 3 are two irrational numbers whose difference is irrational (√3 2) – (√2 – 3) = √3 – √2 2 3 = √3 – √2 5 which is irrational 10Write a pair of irrational numbers whose difference is rational Answer To rationalise the denominator we have to multiply the denominator in negative value to both numerator and denominator such that√5/2√3×2√3/2√3=2√(iv) Multiply both numerator and denominator by 3√52√6 to rationalise the denominator (v) Multiply both numerator and denominator by √48–√18 to rationalise the denominator (vi) Multiply both numerator and denominator by 2√2 – 3√3 to rationalise the denominator Exercise VSAQs Question 1 Write the value of (2 √3) (2
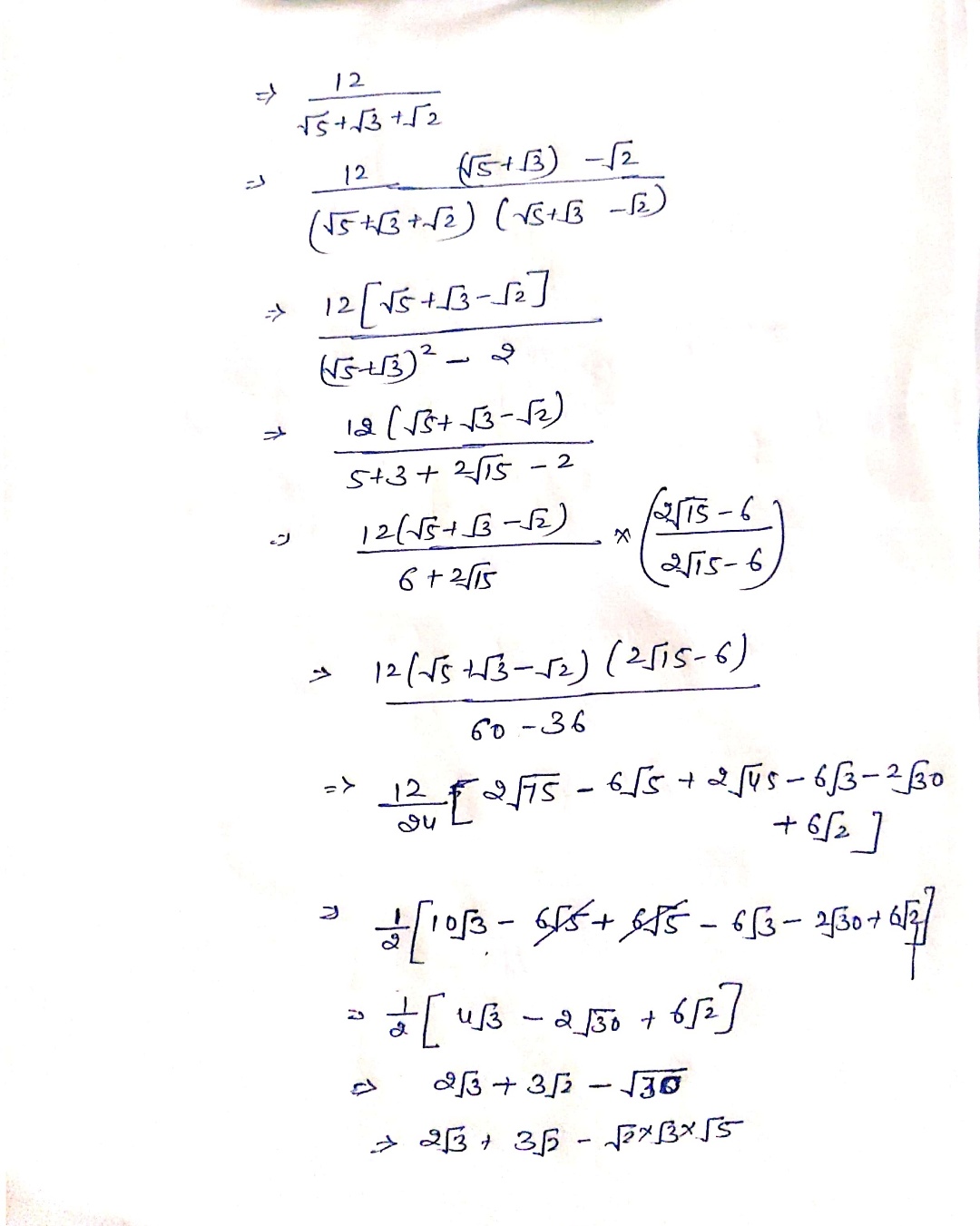



Rationalize The Denominator Of 12 2 3 5




Rationalise The Denominators 1 3 Root 2 2 1 Root 6 Root 5 3 16 Root 41 5 Youtube
Rationalising the denominator Rationalise the denominator, 1) 5 √3 2) 5 √6 3) 2 √3 4) 5 √7 5) 4 √3 6) 4 √6 7) 3 √2 8) 3 √3 9) 4 √2 10) 4 √2 11) 4 Prakhar Bindal answered this Ok Now Lets Divide The Given Expression Into 3 Parts And Solve Them Individually (1 / 2√3) (2 / √5√3) ( 1 / 2√5) = 0 1st Part Rationalising Factor = 2√3 So Lets Rationalise 1 * 2√3) / (2√3 * 2√3) 2√3 / 1 = 2√32/2√3 =2/(2*√3) =1/√3 Ans



Rationalization Of Surds Assignment Point
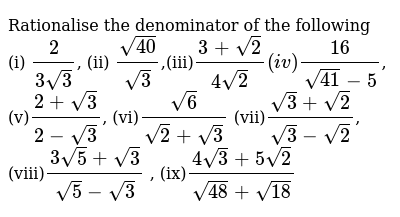



Rationalise The Denominator Of The Following I 2 3sqrt3 I
Multiply both numerator and denominator by 2√2 – 3√3 to rationalise the denominator RD Sharma Solutions for Class 9 Maths Chapter 3 Rationalisation Exercise VSAQs Page No 316{simplify surd expressions involving squares for example √12 = √(4 × 3) = √4 × √3 = 2√3 and rationalise denominators} Pupils should be taught to simplify and manipulate algebraic expressions including those involving surdsTo rationalise surds in the denominator 1 Multiply both numerator and denominator by the surd (in the denominator) 2 Simplify the expression Example A81a Rationalise the denominator of 1 √8 √8 √=22 1 √8 = 1 2√2 Multiply both numerator and denominator by √2 = 1 * √2 2√2 * √2 = √2 4




Rationalise The Denominator Of 1 Root3 Root2 Brainly In
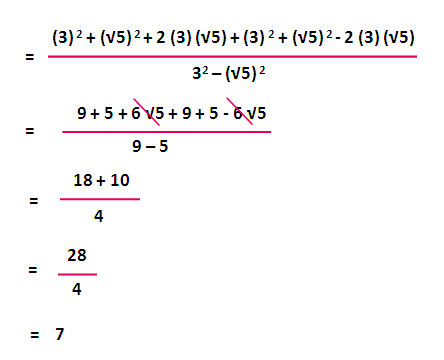



Rationalizing The Denominator With Variables
Example Rationalise the denominator of the following expressions 56 √ 3 2 √ 3 Answer 5 √ 318 6 1√ 2 4 3 √ 2 Answer 107 √ 2 2 =107 √ 2 2 5 Surds and Rationalisation, more practice Example Left to the reader 2Is zero is rational number where q=o e will check if 'View Surdsdocx from MATH IB0085 at Park High School Surds 1 Find the value of k in each of these a) e) √ 8=k √2 √ 300=k √ 3 b) f) √ 50=k √ 2 √ 45=k √ 5 2 Simplify fully, write




If Tan X 1 Simplify Tan Pi 3 X Mathematics Stack Exchange




Simplify By Rationalising The Denominator 2 6 5 3 5 2 6
When we rationalise the denominator, then it becomes easy to find the sum or difference of given fractions For example, 2/√2 is a fraction that has an irrational denominator If we rationalise it, then it becomes √2 Thus, the denominator is a whole number, ie 1 Let us learn in this article how to make the denominator rational with It seems that you know how to rationalise the denominator Hey multiplicative inverse of 2√3 would be 1/2√3=2√3 because sum of two multiplicative inverse results to 1 Hence we can write it in the form cd√3 where c=2 & d= 1 Share Cite Follow Sol 4 / (2 √3 √7) = 4/(2 √3) √7 Rationalising factor of the denominator is (2 √3) √7 = 1/(2 √3) √7 x (2 √3) √7 / (2




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




Rationalize The Denominator Expii




After Rationalizing The Denominator Of 3 12 2 3 And Simplifying We Get 2 6 3 2 M 3 5 Then The Value Of M Is



Rationalise The Denominator In Each Of The Following And Hence Evaluate By Taking 2 1 414 3 1 732 And 5 2 236 Up To Three Places Of Decimal Studyrankersonline




Rationalise The Denominator Of Sqrt 3 Sqrt 2 Sqrt 3 Sqrt




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation Exercise 3 2
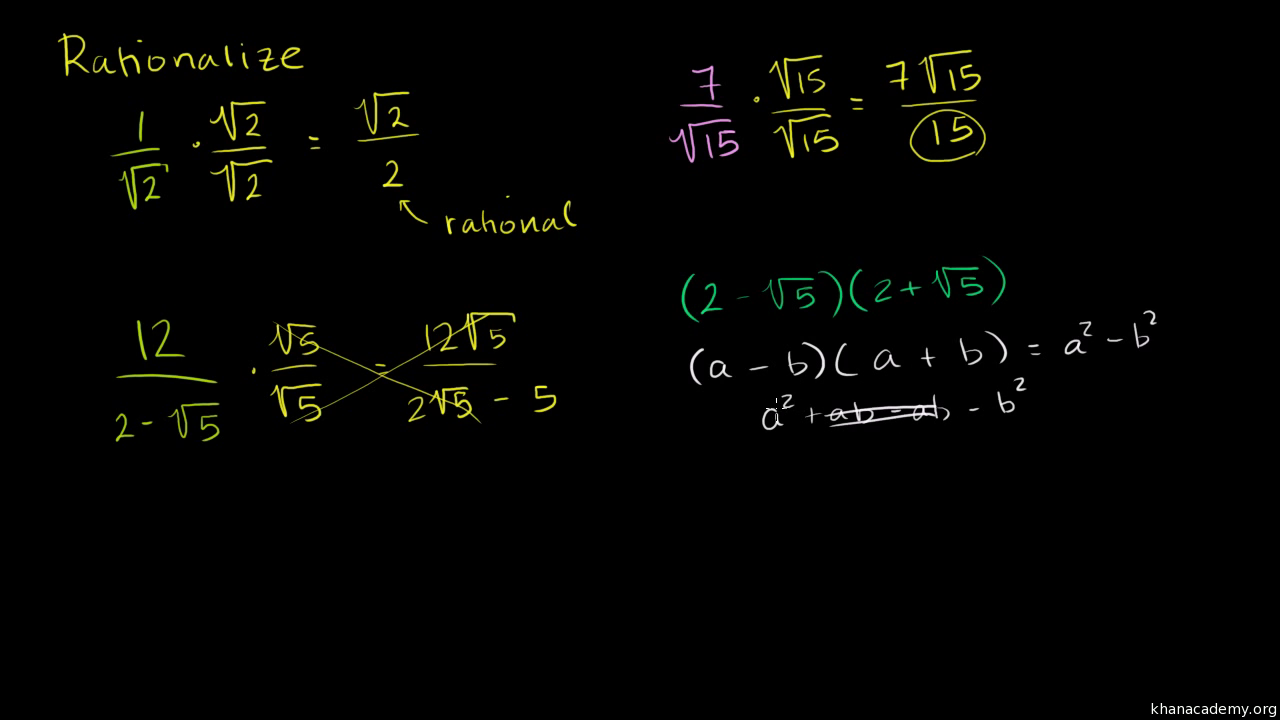



Intro To Rationalizing The Denominator Algebra Video Khan Academy




Simplify By Rationalizing The Denominator 3 5 7 3 3 2 Brainly In




Rationalize The Denominator And Simplify Polynomials Maths Class 9
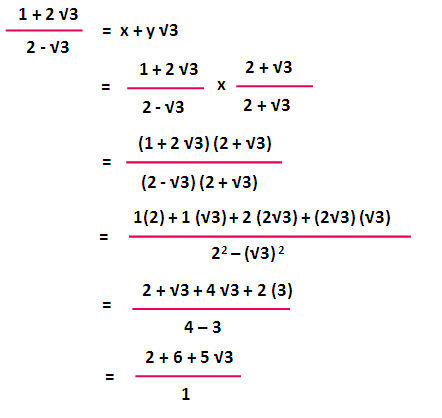



Rationalizing The Denominator With Variables



1




Pin On Tamilnadu Board Class 9 Maths Solutions




2 Write The Lowest Rationalis See How To Solve It At Qanda




Multiplying And Dividing Radical Expressions




Rationalize The Denominator 3 2 5 3 2 Brainly In




Rationalize The Denominator 6 3 2 2 3 Brainly In




Rationalize The Denominator Meaning Methods Examples




How To Rationalize The Denominator 14 Steps With Pictures




Rationalise The Denominator Of 2 3 2 3 Brainly In



Simplifying By Rationalising The Denominator 3 5 3 2 5 3 Studyrankersonline
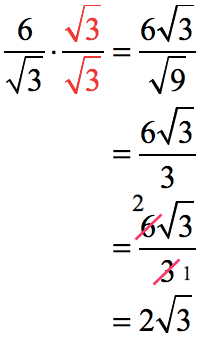



Rationalizing The Denominator Chilimath




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V



Simplifying By Rationalising The Denominator 4 2 3 7 Studyrankersonline




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium
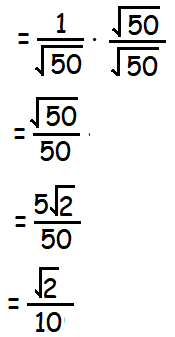



Practice Problems On Rationalizing Denominator




After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is




Intro To Rationalizing The Denominator Algebra Video Khan Academy




Rationalize The Denominator 2 3 5 Brainly In



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community



Simplifying By Rationalising The Denominator 1 3 2 5 Studyrankersonline



2fv5d843v9w22sxtto1ibxtu Wpengine Netdna Ssl Com Wp Content Uploads 15 12 Number H Surds V2 Solutions 1 Pdf



Www Jstor Org Stable 10 4169 Math Mag 2 121




How To Rationalize The Denominator 14 Steps With Pictures




The Simplest Rationalisation Factor Of 2sqrt 2 Sqrt 3 Youtube




Rationalize The Denominator 12 5 3 And Hence Find The Value Of A B In 12 5 3 A 5 B 3




Simplify Math Dfrac 4 Sqrt 3 2 Sqrt 2 Dfrac 30 4 Sqrt 3 Sqrt 18 Dfrac Sqrt 18 3 2 Sqrt 3 Math Quora




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation




Rationalise The Denominator Of 2 Sqrt 3 Sqrt 5 Youtube




The Rationalisation Factor Of 2 Sqrt 3 Is 2 Sqrt 3 B
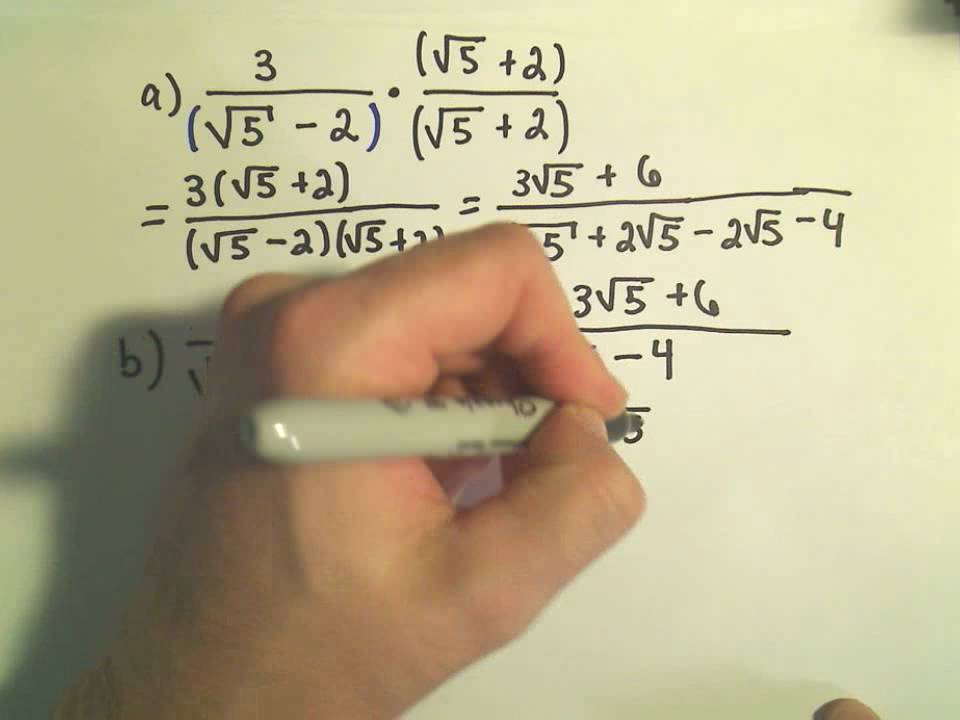



Rationalizing The Denominator Example 1 Youtube




Rationalize The Denominator Expii




How To Rationalize Math Frac 1 Sqrt 2 Sqrt 3 Sqrt 5 Math Quora



Rationalize Denominator 7 3 2 7 3 2 Brainly In




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download
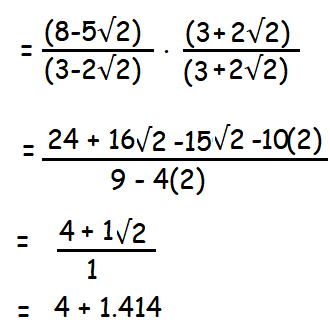



Practice Problems On Rationalizing Denominator




3 2 1 2 5 3 Rationalise This Term In Briefly Brainly In
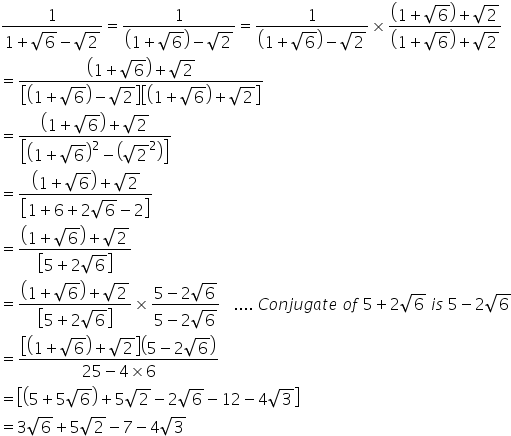



Rationalise The Denominator Of The Expression Mathematics Topperlearning Com Hvx3khh



Rationalise The Denominator Of 1 3 2 And Hence Evaluate By Taking 2 1 414 And 3 1 732 Up To Three Places Of Decimal Studyrankersonline




Rationalise The Denominator Of 5 Sqrt 3 Sqrt 5




Rationalise The Denominator Of 1 2 Sqrt 3 Youtube
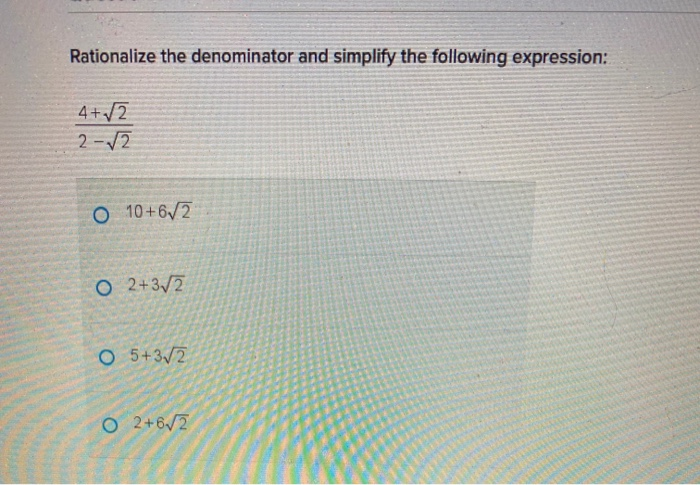



Solved Rationalize The Denominator And Simplify The Follo Chegg Com




Rationalize 2 3 5 2 2 3 3 Brainly In




Chapter 5 Radical Expressions And Equations 5 1




Rationalize The Denominator Meaning Methods Examples




How To Rationalise The Denominator 1 2 3 5 Quora




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Example 2 Rationalize Denominators Of Fractions Simplify Ppt Video Online Download




How To Rationalize Math Frac 1 Sqrt 7 Sqrt 3 Sqrt 2 Math Quora



Q Tbn And9gcssnv O8 K4pkzode39p 4jqc5d5uagpgoo0fmn7ussrbkac4ni Usqp Cau




Rationalise The Denominator 4 3 5 4 3 5 Youtube




Rationalise The Denominator Of 1 7 3sqrt 2



Q Tbn And9gcrdpezo9dtgnwo1evsbut2dx1dc1fff 52tf0 Uifj9lvz9 Uby Usqp Cau




Simplify By Rationalising The Denominator 7 Root 3 5 Root 2 Root 48 Root 18 Youtube



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Rationalize The Denominator Of 3 Minus Root 2 By 3 Root 2 Brainly In



Rationalize The Denominator I 1 5 Ii 2 3 7 Iii 1 3 2 Iv 1 3 5 2 2 V 12 4 3 2 Sarthaks Econnect Largest Online Education Community




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium
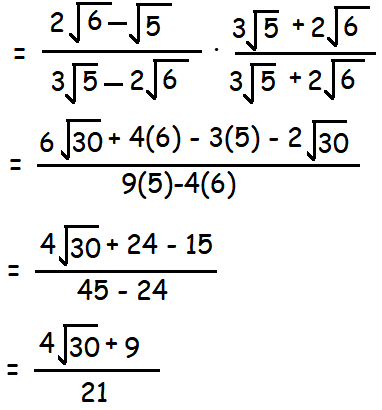



Practice Problems On Rationalizing Denominator




Rationalize The Denominator 4 2 3 7 Maths Polynomials Meritnation Com



How To Rationalize Math Frac 1 Sqrt 7 Sqrt 3 Sqrt 2 Math Quora




Multiplying And Dividing Radical Expressions



1




Rationales The Denominator And Simplify Sqrt 3 Sqrt 2 Sqrt




Rationalise The Denominator 1 3 2 1solve That




After Rationalizing The Denominator Of 2 6 5 3 5 2 6 And Simplifying We Get 9 4 A B Then The Value Of A B Is




Ex 1 5 5 Rationalize Denominators Of I 1 Root 7 Ii 1 Root6




Example 18 Rationalize The Denominator Of 1 2 Root 3




Surds Simplifying A Surd Rationalising A Surd Conjugate




Mathematics 9 Radical Expressions 4




How Do You Simplify The Expression 3 Sqrt5 2 Socratic
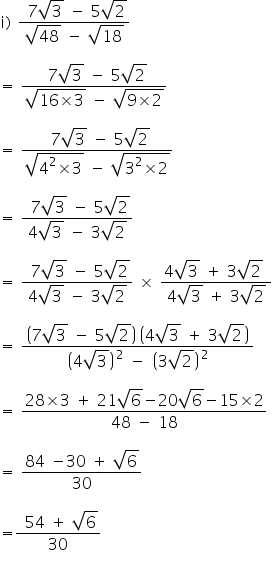



Sir Pls Solve The Following Problem Rationalize The Denominator 7 3 5 2 2 6 5 48 18 3 5 2 6 1 2 3 1 3 2 2 3 1 Mathematics Topperlearning Com Lh6vmmyy



0 件のコメント:
コメントを投稿